Социальное служение Русской Православной Церкви - [электронный ресурс]:

Сложные сети как модели сложных систем¹

Евин И.А.
Московский физико-технический институт (государственный университет)

Введение

Господствующий в современной науке редукционизм, как метод исследования, предполагает, что изучаемая система может быть понята, если описаны и поняты свойства ее элементов. Однако, существует множество так называемых сложных систем, которые не удается формально описать и понять с помощью такого подхода. В самом деле, у больных раком нет отдельного «гена рака», а есть мутации в нескольких десятков взаимодействующих генов. Сознание не может быть сведено к поведению отдельного нейрона, а требует учета взаимодействия миллиардов синапсов. Экономический кризис не будет понят без изучения сложной паутины взаимных задолженностей, свойственных мировой финансовой системе. Изучение причин образования дорожных пробок и нахождение решений для их предотвращения требует изучения структуры всей дорожной сети города.   В этих науках, наряду с парадигмой редукционизма, которая еще отнюдь не исчерпала свой потенциал,  должна иметь место новая  парадигма, отражающая  сложность соответствующих систем[7].

 С конца 1990 годов для изучения сложных систем развивается новый эффективный инструмент исследования – теория сложных сетей. Узлы в таких сетях представляют собой элементы этих сложных систем, а связи между узлами – взаимодействия между элементами[1,5,9,11,17,36]. Такие сети образуют своеобразный каркас соответствующих сложных систем, а исследование свойств этих сетей дает содержательную информацию о свойствах сложных систем в целом, что позволяет преодолеть некоторые недостатки, свойственные редукционизму.

Сетевой подход изучения окружающего нас мира берет свое начало с 1735 года, когда Леонард Эйлер, живший тогда в Петербурге, решил знаменитую задачу о семи мостах в Кенигсберге, и заложил тем самым основы новой математической дисциплины – теории графов. Важной вехой в развитии теории графов стала середина прошлого столетия, когда венгерскими математиками Эрдешем и Реньи была создана теория случайных графов, ставшая основным направлением изучения сетевых структур вплоть до конца двадцатого века [5]. Они ввели в сформировавшуюся к тому времени теорию графов понятия теории вероятности и стали рассматривать семейства графов, а не отдельные графы. Возникновение парадигмы случайных графов можно сравнить с появлением статистической механики на основе механики Ньютона. Иногда случайные графы называют пуассоновскими графами, поскольку вероятностное распределение узлов по числу связей в таких графах подчиняется закону Пуассона.

Очень активно сетевые методы использовались в социологии практически с момента зарождения этой научной дисциплины [36]. Здесь были получены принципиальные результаты и сформулированы важные понятия, востребованные и современной теорией сетей.

Наиболее значительные результаты последних лет в изучении сетевых структур были получены физиками. Оказалось, что методы теоретической физики, прежде всего теории критических явлений, хорошо подходят для изучения проблем в этой области. В отличие от математиков, физики в своих исследованиях опираются на эмпирические данные о реальных сетях, таких как Интернет, Всемирная паутина, сети друзей и знакомых или биологические метаболические сети. В отличие от  социологов, физики изучают статистические свойства сетей, например, законы распределения узлов по числу связей. При изучении этих вопросов были обнаружены универсальные свойства реальных сетей, на которые не обратили внимания математики и социологи. Эти свойства послужили стимулом для разработки новых теорий и моделей, выявления новых фундаментальных свойств сетей. Именно физические журналы в настоящее время публикуют подавляющее число наиболее важных работ в этой области.

Важным фактором интенсификации изучения сложных сетей в последние годы стал высокий уровень развития алгоритмов и компьютерных программ исследования сетей. В последнее время стали доступны многочисленные базы данных реальных сетевых структур: сетей сотрудничества актеров кино и ученых в различных областях науки, сетей белковых взаимодействий и метаболических реакций в живых клетках, нейронная сеть червя нематода C.elegans, а также некоторых технологических сетей, например, сеть примерно пяти тысяч электростанций США. Эти наборы данных позволяют в достаточно полном виде отразить структуру  и функции реальных сложных систем.

Сети «тесного мира»

Социолог из Гарвардского университета Стенли Милграм (Stanly Milgram) в 1967 году эмпирически показал, что любых двух человек на Земле можно соединить цепочкой из шести знакомых [33]. Это утверждение получило широкую известность и стало называться «явлением тесного мира» (small world phenomenon), а после выхода Бродвейской пьесы, а затем и художественного фильма с соответствующим сюжетом, еще и  «шесть рубежей разделения» (“six degrees of separation”) [24].

D 1998 году прикладной математик из Корнельского университета Стивен Строгатц (Steven Strogatz) и его аспирант Данкан Воттс (Duncan Watts) опубликовали в журнале Nature статью, в которой показали, что такие реальные сетевые структуры как сеть нейронных связей червя нематода, сеть актеров Голливуда и сеть из приблизительно 5000 электростанций США также обладают свойством «тесного мира» [46] и имеют при этом высокий коэффициент кластеризации, то есть большое число циклов длины три. Одновременно они предложили математическую модель сетей «тесного мира», свойства которой представляет собой суперпозицию свойств регулярных, периодических решеток и пуассоновских случайных сетей [36].

Меры важности узлов и связей

В современной англоязычной научной литературе по теории сетей понятие важности узла или связи обозначается словом centrality, а в зависимости от подхода к оценке количественной меры важности, к этому слову добавляется  понятие, связанное с сущностью подхода[36].

В современной теории сетей число связей узла называется степенью (degree). Простейшей количественной мерой важности узла, обозначаемой  degree centrality, может служить степень узла, то есть число связей, которые принадлежат данному узлу[22].

Другой мерой важности является betweenness centrality. Этот показатель определяется как доля суммарного числа кратчайших путей между всеми узлами, которые проходят через узел i к общему числу кратчайших путей сети

где  σst (i) – число кратчайших путей из узла s  в узел  t  через узел  i  и σst – общее число кратчайших путей между всеми парами  s  и  t.  Аналогичное определение может быть дано для связей сети.

Betweenness centrality особенно широко используется в изучении транспортных потоков и обычно называется нагрузкой (загруженностью) узла, поскольку характеризует долю проходящих через узел кратчайших путей, и узлы с высоким значением B являются наиболее загруженными. В отличие от степени узла (degree centrality), являющейся локальной характеристикой сети, понятие нагрузки (betweenness centrality) узла или связи отражает топологию всей сети в целом.

Приведем список 10 станций московского метро с наибольшими значениями betweenness centrality[3]:

Таблица 1

Еще одним показателем важности узла может служить показатель closeness centrality, характеризующий среднюю близость к данному узлу всех остальных узлов сети. Формальное определение этого показателя следующее:

«Близость» (closeness centrality) Ci узла i есть величина

где N – общее число узлов в сети, dij – число связей по кратчайшему маршруту между узлами i и j.

В таблице 2 дан список 10 станций московского метро с наибольшими значениями «близости»[3]:

Таблица 2

Closeness centrality, как и betweenness centrality, есть нелокальная характеристика сети.  Существуют и другие меры важности узлов (eigenvector centrality, Katz centrality и т.д.), в том числе меры, разработанные специально для конкретных сетевых структур. Из последних наиболее известна мера PageRank компании Google, созданный для ранжирования по важности сайтов  WWW [36].

Безмасштабные сети

В 1999 году физик из университета Нотр Дам (США) А.-Л.Барабаши (Albert-Laszlo Barabasi) вместе со своей аспиранткой Р.Альберт (Reka Albert) изучали свойства реальных сетей с несколько иной точки зрения. Если Строгатц и Воттс в своем исследовании сетей исходили из феномена «тесного мира», то Барабаши и Альберт решили исследовать закон распределения узлов реальных сетей по числу связей [6,5]. Именно с этой работы теорию сложных сетей стали рассматривать как новый раздел физики.

Для многих сетей (структура Интернета, WWW, сети сотрудничества актеров, сети электростанций США, а также метаболических сети и белковых взаимодействий в клетках, структуры авиационных сообщений в США, и многих других) вместо ожидавшегося распределения узлов по числу связей q по закону Пуассона,   было получено степенное распределение:

где γ – постоянная величина. Для большинства реальных сетей 2 < γ ≤ 3, а само вероятностное распределение более точно описывается формулой

, где q0 и q1 – константы, которая отражает явления насыщения при малых значениях q и обрезания (cut-off) при больших значениях q.

Таким образом, во многих реальных сетях небольшое число узлов содержит очень большое число связей (их называют хабы, от английского слова hub-концентратор), а огромное число узлов содержит лишь несколько связей. Такие сети получили название безмасштабных сетей (scale free networks). Это название не было придумано специально для  этого типа сетей, а было взято из теории критических явлений, где флуктуации в критических состояниях также подчиняются степенному закону, а саму теорию безмасштабных сетей стали рассматривать как один из сценариев выхода сложных систем в критическое состояние. В последнее время такие сети чаще стали называть сложными сетями (complex networks).

Модель Барабаши–Альберт эволюции сетей

Барабаши и Альберт предложили простую и элегантную модель возникновения и эволюции безмасштабных сетей. Они показали, что для возникновения безмасштабных сетей необходимы два условия [5]:

1.Рост. Начиная с небольшого числа m0 узлов, на каждом временном шаге добавляется один новый узел с m (m ≤ m0) связями, которые соединяют этот новый узел с m различными уже существующими узлами.

2. Предпочтительное присоединение (Preferencial attachment).

Когда выбираются узлы, к которым присоединяется новый узел, предполагается, что вероятность  с которой новой узел будет соединяться с уже существующим узлом i, зависит от числа связей qi, которыми этот узел уже связан с другими узлами, так что

Сценарий роста и эволюции безмасштабных сетей, предложенный Барабаши и Альберт, можно отнести к хорошо известному в социологии явлению, получившему название «эффект Матфея», имея в виду библейское выражение «имущему дается…». Есть и другие афористические обозначения этого явления «богатый становится богаче», «деньги к деньгам», «успех порождает успех» и т.д. Этот принцип был взят Прайсом (Derek de Solla Price)[40] и Саймоном (Herbert Simon)[41] для объяснения происхождения степенного закона в социальных явлениях. Физики рассматривают такого рода явления как свойства критических состояний[5,16].

Вычисления показывают, что принцип предпочтительного присоединения действительно приводит к безмасштабной сети с показателем степени γ = 3. Это довольно редко встречающееся в реальных сетях закон распределения, но ценность этой модели  Барабаши-Альберт заключается в том, что она показывает принципиальную возможность генерации безмасштабной сети на базе простых предположений. Рассмотрим, как обобщить эту модель, чтобы получить степенной закон с произвольным показателем степени.

 Пусть вероятность присоединения к узлу степени q пропорциональна функции f(q), которая называется функция предпочтения. В модели Барабаши-Альберт эта функция  есть q. Немного изменим эту функция, пусть она будет линейной: q+A. Здесь A≡ am имеет смысл «дополнительного присоединения», где a >-1 – постоянное число, m- число связей каждого нового узла. Можно показать, что такой линейный закон предпочтений приводит к безмасштабной сети с γ = 3 + a с диапазоном изменений от 2 до бесконечности. Если функция предпочтения имеет вид qθ, где θ – любое вещественное число, можно показать, механизм предпочтительного присоединения генерирует степенное распределение и, соответственно, безмасштабную сеть, только при значении θ = 1, то есть только когда функция предпочтения является линейной [17].

Устойчивость к повреждениям

Исследования показывают, что при произвольном удалении узлов из пуассоновской случайной сети Эрдеша-Реньи, существует определенное критическое значение, измеряемое отношением числа удаленных узлов к общему числу узлов в сети, выше которого сеть распадается на отдельные фрагменты. Для безмасштабных сетей, когда показатель степени γ ≤ 3 такого критического числа не существует[5,35].  Следовательно, такие безмасштабные сети очень устойчивы к случайным повреждениям или внешним случайным воздействиям. Эта устойчивость объясняется негомогенной топологической структурой этих сетей. Однако, у таких сетей существует своеобразная «Ахиллесова пята»[5] – целенаправленное повреждение одного или нескольких узлов с большим числом связей (degree centrality) ведет к дезинтеграции сети. Например, хакер может существенно повредить WWW, если выведет из строя один или несколько  сайтов с большим числом связей.

С проблемой устойчивости сети при случайных повреждениях тесно связана задача исследования распространения инфекции: как распространение вирусов в сети WWW, мобильных телефонов или электронной почты, так и распространение вирусов биологической природы в социальных сетях[36]. Низкая величина скорости распространения заболевания соответствует высокой доле удаленных узлов или связей гигантской связанной компоненты сети в случайно поврежденной сети. Отсутствие эпидемического порога означает невозможность разбить гигантскую связанную компоненту на отдельные фрагменты случайным удалением узлов или связей в бесконечных сетях. Если сеть конечна, а все реальные сети конечны, то гигантская связанная компонента может быть дезинтегрирована случайным удалением достаточно большой, но конечной доли узлов, и, следовательно, эпидемический порог существует.

Каскадные повреждения  в техногенных системах

В сложных техногенных системах могут возникать катастрофические нарастающие явления, инициированные небольшой долей составляющих эти сложные системы элементов. Примерами таких лавинообразных процессов могут служить каскадное отключение электричества, как это имело место, например, на западе США и Канады 14 августа 2003 года при повреждении на одной из электростанций в Огайо, когда миллионы людей около 15 часов оставались без света.

Каскадные отключения в сети электростанций есть результат лавинообразного распространения перегрузки, возникшей в одном из узлов этой сети. Моттер и Лэй предложили простую модель этого процесса [34]. Нагрузка узла сети в этой модели – это та нагрузка узла (betweenness centrality), определение которой было дано выше. Для каждого узла i этой сети вводится предельная нагрузка – емкость узла:

ci = (1+α)b0i,

где b0i – нагрузка (betweenness centrality) этого узла в неповрежденной сети, а константа α ≥ 0 есть «параметр устойчивости», показывающий насколько первоначальная нагрузка может быть превышена. Каскадное отключение в этой модели выглядит следующим образом:

1.Удаляем узел. Это приводит к перераспределению нагрузок у других узлах: b0i → b0i.

2. удалить все перегруженные узлы, то есть узлы, для которых b0i > ci

3. повторить эту процедуру до тех пор, пока остаются перегруженные узлы.

При моделировании этого процесса в различных сетях Моттер и Лей вычисляли отношение G = Nafter/ N, где N и Nafter – соответственно начальное число узлов и размер наибольшей связанной компоненты после каскадного отключения (имея в виду, что начальное число узлов совпадает с гигантской связанной компонентой первоначальной сети). Результирующее значение G(α) зависит от архитектуры сети, параметра α и характеристик первого отключенного узла, в первую очередь от его степени, то есть числа связей. В случайном графе для любого значения α > 0 G = 1 и только если α = 0, сеть полностью выведена из строя, G = 0.

С другой стороны, в сетях со степенным законом распределения узлов по числу связей величина G строго зависит от степени, а также от нагрузки первого удаленного узла. Моттер и Лэй исследовали свойства безмасштабной сети с γ = 3. Значение α = 0 дает G = 0 при любом начальном узле для любой сети, в то время как α → ∞ дает . Вопрос заключается в том, как выглядит зависимость G(α) при промежуточных значения α. Когда первый удаляемый узел выбирается случайно, каскад будет большим (G сильно отличается от единицы) только при малых значениях α, а G(α) быстро растет при изменении α от 0 до 1. Если же начальный узел выбран среди хабов, то G растет медленно с ростом α, а каскады могут быть очень большими даже при относительно больших значениях α.

Ли с сотрудниками численно исследовали статистику каскадов этой модели на безмасштабных сетях с 2 < γ ≤ 3 и обнаружили, что в этом случае имеется критическая точка αc≈ 0.15 [29]. При α < αc развиваются гигантские лавины, а при α > αc размеры лавин существенно меньше. В самой критической точке распределение лавин по размерам подчиняется степенному закону

, где τ ≈ 2.1 во всем диапазоне 2 < γ ≤ 3.

С. Булдырев (Sergey Buldyrev) с коллегами исследовали поведение сложной системы состоящей из двух сетей А и В, причем определенная доля узлов сети А cвязана с узлами сети В, а некоторая доля узлов сети В связана с узлами сети А [10]. Такие сети получили название взаимозависимые сети (interdependent networks). Если узлы в одной из этих сетей выходят из строя, это может вызвать выход из строя узлов в другой сети, а это повлечет за собой итерационное каскадное повреждение узлов в обеих сетях. Достигнув определенного критического значения отношения вышедших из строя узлов к общему числу узлов, происходит фазовый переход первого рода, когда возникает скачкообразный полный распад и выход из строя обеих сетей А и В, а, значит, и всей системы в целом.

Численные и аналитические исследования показывают, что при уменьшении силы связи между узлами А и В, происходит переход от перколяционного фазового перехода первого рода к переходу второго рода.

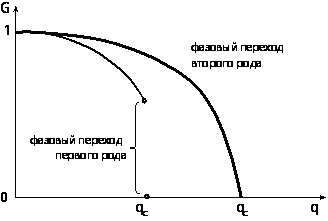Рисунок 1

Перколяционные фазовые переходы первого и второго рода в каскадных процессах в сложных сетях.  Величина G есть доля от общего числа соединенных узлов в сложной сети состоящей из двух сетей, часть узлов которых связаны между собой, q есть доля  узлов удаленных из сети, а qc есть критическое значение этой доли, при котором происходит распад всей сложной сети на фрагменты (G=0). При слабых связях между двумя сетями полная фрагментация происходит непрерывно (синяя кривая), а при сильных связях такой переход происходит скачком, аналогично тому, как происходит фазовый переход первого рода.

Как говорилось выше, безмасштабные сети очень устойчивы к случайным повреждениям. Однако, если сложная сеть состоит из двух и более тесно связанных между собой безмасштабных сетей, то в такой системе полная фрагментация наступает выше некоторой достаточно малой доли удаленных (отключенных) узлов и такое переход также происходит скачком, как в переходах первого рода.

В реальных сетях такого рода каскадные отключения произошли в Италии 28 сентября 2003 года, когда повреждения на одной из электростанций вызвало отключения некоторых узлов сети Интернет, что в свою очередь вызвало дальнейшие отключения электростанций [10].

Функциональные сети мозга

Покажем на примере мозга возможный подход изучения сложных систем на основе теории сложных сетей. Мозг человека, состоящий из нескольких десятков миллиардов нейронов, является одной из наиболее сложных систем в природе. В мозге постоянно идут процессы самоорганизации и распада функциональных нейронно-сетевых структур. Каждая такая сеть, объединяющая нейронные ансамбли из разных отделов мозга,  создается для реализации определенной функции мозга – поведенческой, когнитивной и т.п. Именно такие функциональные нейронные сети стали объектом изучения группы исследователей во главе с Д.Чиалво (Dante Chialvo), целью которых было проверить возможность приложения идей и методов современной теории сетей (безмасштабные сети, сети «тесного мира» и т.д.) к топологии реальных функциональных  структур мозга [19].

Используя метод магнитно-резонансного изображения, измерялась активность мозга при осуществлении простого моторного действия (стук пальцем по столу) на каждом временном интервале в 2,5 секунды на протяжении 400 таких интервалов. Изучалась область мозга размером 36×64×64 пространственных ячеек с размером каждой ячейки 3×3,475×3,475 мм 3.

Обозначим активность каждой такой ячейки  в момент времени t  как V(x,t). Каждые две ячейки будем считать функционально связанными между собой, если значение пространственно-временной корреляции r(x1,x2) между ними превышает некоторый порог rc. Само значение корреляции вычисляется по следующей формуле

Где σ2(V(x)) = ‹V(x,t)2› – ‹V(x,t)›2 , а ‹·› означает усреднение по времени.

Разделив мозг на тысячи ячеек, фиксировалась активность каждой такой ячейки при выполнении таких простых функций как, например, стук пальцем по столу. При регистрации активности каждой такой ячейки можно определить, какие ячейки взаимосвязаны между собой (если активность ячеек в разных частях мозга проявляет свойство синхронности, то это указывает на то, что между ними есть связь). Полная сеть содержит N = 31503 узла. Оказалось, что такие связанные ячейки образуют безмасштабную сеть с законом распределения узлов по числу связей 

где γ ≈ 2.

Рисунок  2.  Функциональная сеть мозга человека при выполнении им простого моторного действия. Показан фрагмент такой сети.

В настоящее время это направление изучения мозга как сложной сети стало одним из наиболее плодотворным [42]. Аналогичные подходы развиваются для задач диагностики сердечно-сосудистых заболеваний[30].

Социальные сети

Сложные сети принято разделять на технологические (Интернет, WWW, сети электростанций, транспортные сети),  биологические (экологические сети, сети белковых взаимодействий, метаболические сети) и социальные (сети друзей и знакомых, сети сотрудничества, сети цитирования, сети мобильной телефонной связи). При этом технологические и биологические сети отличаются от социальных сетей характером корреляции узлов, который получил название ассортативность. Показатель ассортативности описывается коэффициентом Пирсона:

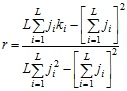Здесь L число связей в сети, а ji и ki – число связей у узлов на обоих концах связи i. Если узлы с большим числом связей (хабы) связаны друг с другом, то r ≈ 1. Если узлы с большим числом связей связаны с узлами с небольшим числом связей, то r ≈ -1. У биологических и социальных сетей разные знаки показателя ассортативности. В социальных сетях имеет место положительная ассортативность, для технологических и биологических сетей свойственна отрицательная ассортативность [36].

Из всех типов сетей социальные сети имеют наиболее длительную историю изучения. Именно в социальных сетях в 1965 году Д.Прайсом был впервые эмпирически обнаружен степенной закон распределения узлов по числу связей[39]. Открытие в социальных сетях явления «тесного мира» С.Милграмом стало решающим фактором развития современной теории сложных сетей.

Важные явления и закономерности были обнаружены и исследованы в социальных сетях друзей и знакомств в последние годы. Оказалось, например,  что в сетях друзей действует закон трех рубежей влияния: наше влияние распространяется только на наших друзей и друзей наших друзей. На следующем шаге это влияние уже ничтожно мало. Обратное также справедливо: наибольшее влияние на нас оказывают наши друзья и друзья наших друзей[13].

Еще на ранних этапах развития теории сложных сетей были детально исследованы законы распространения инфекционных заболеваний в социальных сетях, в том числе в сетях друзей и знакомых[9]. Исследования последних лет показали, что аналогичным образом распространяются в социальных сетях хорошее настроение (happiness) и депрессия, курение, алкоголизм, ожирение, и даже суицидальное поведение[13-15,23].

Литературные персонажи не образуют социальные сети

Персонажи литературных романов также образуют сети друзей и знакомых, и мы решили выяснить, являются ли соответствующие структуры социальными сетями. В Таблице 1 представлены данные по числу персонажей и показателю ассортативности четырех известных литературных произведений. Как мы видим, ни одну из сетевых структур взаимосвязи персонажей этих произведений по характеру корреляции узлов (во всех случаях величина корреляции оказалась отрицательной) нельзя отнести к социальным сетям.

Таблица 1.  Сравнительные характеристики сетевых структур персонажей некоторых произведений мировой литературы. Данные по сетевым структурам персонажей получены из [14].

Автор и название литера-турного произведения	Число персонажей	Ассортативность r
Л.Н. Толстой “Анна Каренина”	138	-0,307
М.Твен “Геккельбери  Финн”	74	-0,132
Ч.Диккенс “Дэвид Копер-фильд”	87	-0,236
В.Гюго “Отверженные”	80	-0,165

Мак Каррон (Padraig Mac Carron)  и Кена (Ralph Kenna) проанализировали некоторые статистические свойства сетевых структур персонажей англосаксонской эпической поэмы XI века “Беофульф” (Beowulf) , ирландского эпоса VIII века “Похищение быка из Куальнга”  (Tain Bo Kuailnge), а также “Илиады” Гомера. Результаты по ассортативности даны в Таблице 2

Таблице 2. Ассортативность сети персонажей некоторых произведений древней мифологии [16].

название мифологического произведения	Число персонажей	Ассортативность r
“Илиада”	561	-0,117
“Беовульф”	74	-0,100
“Тейн”	404	-0,330

Таким образом, сетевые структуры взаимоотношений персонажей этих произведений также нельзя отнести к социальным сетям.

Взаимодействие персонажей Нового Завета  в определенной степени отражает реальные исторические события,  и по этой причине можно было бы ожидать, что соответствующие социальные взаимодействия формирует сеть c положительной ассортативностью. Однако проведенные нами расчеты ассортативности сети  взаимоотношений Иисуса с другими персонажами Нового Завета дает значение -0,133 , что также означает, что эта сеть не является социальной, то есть закон ее формирования не соответствует принципу “подобное стремится к подобному” (Рисунок 3) .

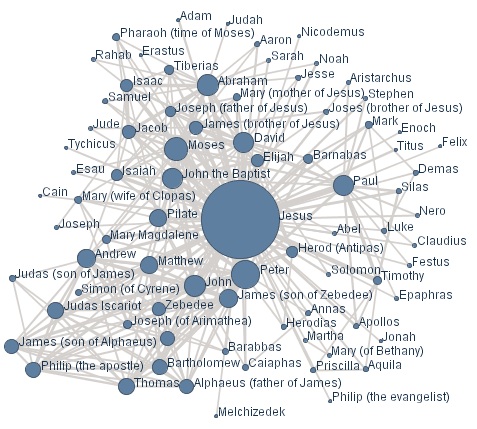Рисунок 3. Сетевая структура взаимоотношений персонажей Нового Завета имеет отрицательный коэффициент корреляции между узлами, равный – 0,133 и, следовательно, не является социальной

На протяжении трех тысяч лет писатели, поэты, художники, композиторы используют в своем творчестве мифологические образы Древней Греции. Возможно, и сейчас эти сюжеты и образы формируют нас в большей степени, чем современная литература.

На основе словаря классической греческой мифологии Гранта и Хазеля [17] была сконструирована ориентированная сеть межличностных связей героев древнегреческих мифов [18]. В этой сети каждому узлу соответствует определенный персонаж, а узлы А и В соединены связью, если при описании персонажа А появляется персонаж В, и наоборот. Сети персонажей литературных произведений, сеть персонажей Нового Завета, а также сеть героев древнегреческих мифов являются когнитивными и хранится в памяти миллионов людей.

В полученной сети  1647 узлов, которым соответствуют  боги, нимфы, чудовища, сирены, простые смертные.  Эта сеть оказалась безмасштабной с суммарным показателем степени γ = 2,63. Наибольшее число связей оказалось у Зевса – 243, и у Геракла – 230. К сожалению, авторы этой работы не вычисляли показатель ассортативности сети героев греческой мифологии, а также недостаточно полно изучена ее модулярная структура.

Сети популярности объектов живописи, скульптуры и архетиктуры

Важной проблемой в эстетике является количественное изучение популярности объектов живописи, скульптуры и архитектуры. Шич (Maximillian Schich), Леман (Sune Lehman) и Парк (Juyong Park) из Бостона показали, что многие каноны скульптуры и архитектуры, сформировавшиеся в эпоху Европейского Ренессанса можно связать с   объектами античного искусства, которые стали известны в эту эпоху. Такие  исследования стали возможны благодаря завершению формирования к 2005 году (эта работа началась в 1947 году) соответствующих баз данных (CENSUS 2005), в которых были классифицированы огромное количество изображений произведений античного искусства и их фрагментов на основании документов, известных в период с 1400 по 1600 годы.

Структуры, полученные в этих исследованиях, могут быть интерпретированы как двудольные сети, соединяющие документы, известные во времена Европейского Ренессанса,  с изображениями произведений искусства античности отобранных на основе определенных критериев классификации. Исследования показывают, что такие двудольные классификационные сети являются безмасштабными сетями с распределением связей по степенному закону. Были также обнаружены степенные законы распределения популярности для отдельных фрагментов храмов, скульптур, саркофагов, деталей колонн и т.п., что показывает универсальный характер обнаруженных количественных закономерностей.

Авторы данного исследования рассматривают его как новый подход к проблеме формирования канона и изучению его свойств. Однако, эта работа имеет важное значение и для когнитивных наук, поскольку  дает новый подход к  пониманию закономерностей формирования  визуальных стереотипов и их смысловых отображений  в различных документах.

Заключение

Некоторые исследователи, сравнивают важность теории сложных сетей и развиваемые в рамках этой теории технологические приложения для научно-технического прогресса в XXI веке, с квантовой механикой в прошлом веке [35]. Именно квантовая механика стала главной научной основой технологических достижений в XX веке: атомная энергетика, транзисторы, сотовые телефоны,  и т.д.  В настоящее время теория сложных сетей продолжает развиваться как новый раздел статистической физики и уже сейчас без этой теории невозможен эффективный поиск лекарственных препаратов, изучение функций мозга [20], исследования по безопасности сложных технических объектов [1].

Ожидается, что в ближайшее время будет преодолен разрыв между обнаруженными  универсальными эмпирическими закономерностями в сетевых структурах реальных объектов и пониманием самой природы сложных систем, способностью прогнозировать их поведение.

Литература

1. Евин И.А. Введение с теорию сложных сетей. //Компьютерные исследования и моделирование. 2010, Том 2, N2, с. 121-141
2. Евин И.А., Кобляков А.А., Савриков Д.В, Шувалов Н.Д.. Когнитивные сети. //Компьютерные исследования и моделирование. 2011,  Т. 3 № 3 С. 231–239
3.  Евин И.А., Чернобровкин Д.А. Уязвимость и надежность метрополитена как сложной транспортной системы. Проблемы безопасности и чрезвычайных ситуаций. 2011, N 5, с.107-113
4. Adamic L.A. and Glance N. The political Blogosphere and the 2004 U.S. Election: Divided They Blog. Proceedings of the 3rd International Workshop on Link Discovery (New York: Association for Computing Mashinery, 2005), 36-43
5. Albert R., Barabasi A.-L. Statistical mechanics of complex networks, // Rev. Mod. Phys. 74, 47, 2002; arXiv:cond-mat/0106096.
6. Barabási, Albert-László and Réka Albert, Emergence of scaling in random networks, Science, 286:509-512, October 15, 1999
7. Barabási A.-L The network takeover,  Nature Physics 8, 14•16, 2011/12/22
8. Barthelemy M. Spatial Networks. Physics Reports, Volume 499, Issue 1-3, p. 1-101.
9. Boccatti S., Latora V., Moreno Y., Chavez M., Hwang D.-U. Complex Networks: Structure and Dynamics. // Physics Reports, 424, 175-308 , 2006
10. Buldyrev S., Parshani R., Paul G., Stanley H., Havlin Sh.. Catastrophic cascade of failures in interdependent networks. // Nature, Vol. 464|15 April 2010, pp.1025-1028
11.  Caldarelli G. Scale-Free Networks. Complex Webs in Nature and Technology. Cambridge University Press. 2007.
12. Choi Y.-M., Kim H.-J. A directed network of Greek and Roman mythology. // Physica A 382, 665–671, 2007
13. Christakis N.F and Fowler J.H. Connected. Back Bay Books. New York, 2009
14.  Christakis, N. A.; Fowler, JH (22 May 2008). The Collective Dynamics of Smoking in a Large Social Network. New England Journal of Medicine 358 (21): 2249–2258
15.  Christakis, N. A.; Fowler, JH (26 July 2007). The Spread of Obesity in a Large Social Network Over 32 Years. New England Journal of Medicine 357 (4): 370–379
16. Dorogovtsev S. N. Goltsev A. V., Mendes J. F. F. Critical phenomena in complex networks. // Rev. Mod. Phys. 80, 1275, 2008. arXiv:0705.0010v6 [cond-mat.stat-mech]
17. Dorogovtsev S. N. Lectures on Complex Networks, Oxford University Press, Oxford, 2010
18. Dorogovtsev S.N, Mendes J.F.F. Evolution of Networks: From Biological Nets to the Internet and WWW, Oxford University Press, Oxford, 2003
19. Eguiluz V.,ChialvoD.,  Cecchi G.,  Baliki M.,  and  Apkarian V. Scale-free brain functional networks. //Physical Review Letters.  2005, 94, 018102
20.  Ferrer I Cancho R. and Sole R. Small world of human language. //Proc.Royal Soc. B. 2001, 268, 2261,
21. Fouler J.H. Turnout in a Small World. In “The Social Logic of Politics: Personal Networks as Contexts for Political Behaviour”. Ed. A.Zuckerman (Philadelphia: Temple University Press, 2005): 269-287
22.  Fouler J.H. Connecting the Congress: A Study of Cosponcorship Networks. Political Analysis. 14 (2006): 456-487
23.  Fowler, J. H.; Christakis, N. A (3 January 2009). “Dynamic Spread of Happiness in a Large Social Network: Longitudinal Analysis Over 20 Years in the Framingham Heart Study” . British Medical Journal 337 (768): a2338.
24.  Guare J. Six Degrees of Separation. Vintage Books, New York, 1990.
25. Huckfeldt R. and Sprague J. Citizens, Parties, and Social Communication. New York. Cambridge University Press. 1995.
26.  Jiang B. and Claramunt C. Topological analysis of urban street networks. Environment and Planning B: Planning and Design.  2004, volume 31, pages 151-162
27. Kelly J. and Etlig B. Mapping Iran’s Online Public: Politics and Culture in the Percian Blogosphere. Berkman Center Research Publication 2008-01 (2008): 1-36
28.  Lazarfeld P.F., Berelson B., and Gaudet H. The People’s Choice. New York. Columbia University. 1944
29.  Lee E. J., Goh K.-I., Kahng B., Kim D., 2005, Robustness of the avalanche dynamics in data packet transport on scale-free networks. Phys. Rev. E 71, 056108
30.   Li Xiang and Dong Zhao. Detection and prediction of the onset of human ventricular fibrillation: An approach based on complex network theory. Physical Review  E 84, 062901 (2011)
31. Liu X., Tse C.K., Small M. Complex network structure of musical compositions: Algorithmic generation of appealing music. // Physica A 389,  126-132, 2010
32. Masucci A.P. and Rodgers G.J. Network properties of written human language. //Physical Review E 74, 026102, 2006
33. Milgram S. The small world problem // Psychology Today.  № 2. Р. 60–67, 1967
34. Motter A. E., Lai Y.-C., 2002. Cascade-based attacks on complex networks. // Phys. Rev. E, 66, 065102.
35.  Newman M.E. J. The Physics of Networks. // Physical Today. November,33-38, 2008
36.  Newman M. Networks. An Introduction. Oxford University Press, 2010
37. Nickerson D.W. Is Voting Contagious? Evidence from Two Field Experiments. American Political Science Review. 102 (2008):49-5
38. Porta S. , Crucitti P., Latora V. The network analysis of urban streets: A dual approach. Physica A 369 (2006) 853–866
39.  Price D. Networks of Scientific Papers. // Science 149 (3683):510-515, 1965.
40.  Price D. A General Theory of Bibliometric and other Cumulative Advantage Processes. J. Amer. Soc. Inform. Sci. 27, 292-306 (1976)
41.  Simon H. A. On a Class of Skew Distribution Functions. Biometrica 42, 425-440 (1955)
42. SpornsO. Networks of the Brain. The MIT Press. 2011.
43. Proceedings of the National Academy of Sciences 101, 17940-17945 (2004)
44.  Watts, D.J.; Strogatz, S.H. Collective dynamics of  ’small-world’ networks. //Nature 393, 1998.

---